5.7. Monotone und beschränkte Folgen
Im letzten Abschnitt konnten wir bequem und schnell über das Grenzwertverhalten von Folgen entscheiden. Die Grenzwertsätze lieferten die nötigen Techniken. Allerdings ist der Bereich der Folgen, die mit dieser Methode bearbeitet werden können, deutlich eingeschränkt, denn die Folgen müssen ja eine bestimmte Struktur aufweisen. Es ist daher sinnvoll, nach weiteren Konvergenztests zu suchen.
Wir greifen noch einmal die Eigenschaften monoton und beschränkt auf. Beide haben allein keinen bzw. nur einen geringen Bezug zur Konvergenz. Ihre Kombination aber ist überraschenderweise sehr günstig und liefert ein oft benutztes Konvergenzkriterium.
Im Unterschied zu den Grenzwertsätzen allerdings gibt es keine Auskunft über den Grenzwert selbst.
Außerdem ist seine Gültigkeit streng an die reellen Zahlen gebunden; auf Folgen in etwa, ist es nicht anwendbar (siehe [5.7.11]).
|
Satz: Für jede reelle Zahlenfolge gilt:
Ist monoton und beschränkt, so ist auch konvergent.
|
[5.7.1] |
Beweis: Wir führen den Beweis für eine monoton wachsende Folge.
Zunächst gibt es auf Grund der Beschränktheit ein , so dass
.
Die Menge der Folgenglieder ist also eine nicht-leere, nach oben beschränkte Teilmenge von . Sie besitzt - und hier geht die Besonderheit der reellen Zahlen ein - nach dem Vollständigkeitsaxiom eine kleinste obere Schranke, das Supremum also. Wir setzen nun und zeigen:
Sei dazu ein
vorgegeben. Da g die kleinste obere Schranke von ist, kann keine obere Schranke mehr sein. Es muß also mindestens ein Folgenglied oberhalb von liegen, d.h. es gibt ein , so dass .
Beachtet man, dass g auch eine gewöhnliche obere Schranke der monoton wachsenden Folge ist, so erhält man für alle :
,
also . Gemäß [5.4.2] ist dies die Behauptung.
|
Bei der Anwendung des neuen Kriteriums "monoton und beschränkt" gehen wir stets in zwei Schritten vor: Zunächst erhalten wir die reine Konvergenzaussage, anschließend ermitteln wir den Grenzwert selbst.
In einem ersten Beispiel studieren wir Folgen des Typs .
|
Bemerkung: Für hat man:
-
|
|
[5.7.2]
|
-
|
ist divergent
|
[5.7.3]
|
Beweis:
|
1. ►
|
Nach [5.5.6] reicht es zu zeigen, so dass wir o.E. annehmen dürfen. Wir multiplizieren diese Ungleichung mit und erhalten
.
ist also monoton fallend und beschränkt, somit konvergent, etwa gegen g.
Bleibt zu zeigen . Dazu betrachten wir zusätzlich die Folge , die ebenfalls gegen g konvergiert, und benutzen einen kleinen Trick, indem wir den Grenzwert von über den dritten Grenzwertsatz ein zweites Mal berechnen. Also:
Da aber genau einen Grenzwert hat, muss gelten, also , denn nach Voraussetzung ist .
|
|
2. ►
|
Für , etwa mit einem , folgt mit der Bernoullischen Ungleichung
Mit ist daher auch unbeschränkt, also divergent.
|
|
Beachte:
Wir setzen das Kriterium erneut ein, um den bekannten Konvergenzen weitere hinzuzufügen.
|
Bemerkung: Für und gilt:
-
|
|
[5.7.4]
|
-
|
|
[5.7.5]
|
Beweis:
|
1. ►
|
Die Monotonie des Wurzeloperators liefert für alle die folgenden Ungleichungen:
ist also monoton fallend und beschränkt, somit konvergent, etwa gegen g. Zur Ermittlung von g nutzen wir den dritten Grenzwertsatz:
|
|
2. ►
|
Wir setzen wieder den dritten Grenzwertsatz ein und benutzen das Ergebnis aus 1.:
|
|
Das nächsten Beispiel ist klassisch. Es führt uns zu einer der wichtigsten mathematischen Konstanten, der sog. Eulerschen Zahl.
|
Beispiel:
-
und sind konvergent.
|
[5.7.6] |
Beweis: Beide Konvergenzaussagen lassen sich am besten gleichzeitig beweisen.
Wir zeigen in drei Schritten dass beide Folgen monoton und beschränkt sind:
|
1. ►
|
ist monoton wachsend, denn mit der Bernoullischen Ungleichung erhalten wir für zunächst
und daraus:
.
|
|
2. ►
|
ist monoton fallend: Wir setzen noch einmal die Bernoullische Ungleichung ein und erhalten für
Damit können wir jetzt folgendermaßen abschätzen:
|
|
3. ►
|
und sind beschränkt, denn da und folgt aus dem gerade gezeigten Monotonieverhalten:
.
|
|
Beachte:
Da besitzen und über [5.7.6] hinaus sogar denselben Grenzwert! Die Zahl
|
|
[5.7.7] |
heißt die Eulersche Zahl. Wir werden ihr noch oft begegnen und neben [5.7.7] weitere Berechnungsmöglichkeiten finden. Leonhard Euler selbst berechnet in seinem 1748 veröffentlichten Werk
Introductio in Analysin infinitorum bereits die ersten 18 Stellen der Eulerschen Zahl: e = 2.718281828459045235....
Dabei hat Euler bei seiner Berechnung sicherlich nicht die Darstellung in [5.7.7] benutzt, denn wie man im folgenden Applet selbst ausprobieren kann, konvergiert z.B. die Folge äußerst langsam. So sichert etwa
Im übernächsten Abschnitt geben wir eine Folge an, die deutlich schneller gegen e konvergiert. Mit ihrer Hilfe gelingt auch der Nachweis, dass die Eulersche Zahl irrational ist.
Über die Beschränktheit von , etwa nach oben durch 4, gewinnen wir die Konvergenz einer weiteren, nicht elementaren Folge.
|
Beispiel:
-
|
[5.7.8] |
Beweis: Da , gilt für alle der Reihe nach:
ist also monoton fallend und wegen auch beschränkt, und somit konvergent etwa gegen . Dabei können wir den Fall ausschließen,
denn da archimedisch geordnet ist, finden wir zu jedem ein , so dass . Das allgemeine Binomialtheorem [5.2.5] ermöglicht nun für dieses n die folgende Abschätzung:
.
Also hat man , und damit , denn man weiß, dass ist.
|
Die Konvergenz von zieht weitere Konvergenzen nach sich. Für hat man , so dass aus dem Schachtelsatz [5.5.8] folgt
|
[5.7.9] |
Dies gilt dann auch für : .
Mit weiteren Beispielen zeigen wir die Bedeutung des Kriteriums "monoton und konvergent" für die Untersuchung rekursiver Folgen auf.
|
Beispiel:
Beweis: Wir zeigen zunächst per Induktion, und damit ist bereits beschränkt,
►
► Aus erhält man die Abschätzung
und hat damit .
Ferner ist monoton fallend, denn mit hat man auch , so dass mit der folgenden Äquivalenz die Behauptung bewiesen ist:
Insgesamt ist daher konvergent, etwa gegen . g ist aber auch Grenzwert von , so dass wir g auch mit Hilfe der Grenzwertsätze berechnen können:
Grenzwerte sind eindeutig, also hat man die Gleichung und damit (beachte ):
|
Das letzte Beispiel ist ein sehr nützliches Hilfsmittel zur approximativen Berechnung von Quadratwurzeln. Wie der Name verrät, ist dies ein sehr altes Verfahren.
|
Bemerkung (Babylonisches Wurzelziehen): Ist , so ist für jeden Startwert die durch die Rekursion gegebene Folge konvergent, genauer:
|
[5.7.10] |
Beweis: Zunächst vergewissern wir uns durch eine induktive Überlegung, dass für alle n. Da Quadrate stets positiv sind, liefert uns der Schluss
die Abschätzung . Für alle gilt daher:
Also ist monoton fallend und wegen auch beschränkt, insgesamt daher konvergent, etwa gegen . Da auch können wir zur Ermittlung von g wieder unseren "Standardtrick" einsetzen: Aus
erhalten wir dabei .
|
Beachte:
Das Grundprinzip des Babylonischen Wurzelziehens ist einfach und genial zugleich. Die Äquivalenz
lesen wir so: Ist zu klein (zu groß), so ist zu groß (zu klein). In jedem Fall ist daher das arithmetische Mittel ein vermutlich besser Approximationswert.
Ist a rational, so zeigt ein einfacher Induktionsbeweis, dass eine Folge in ist. Insbesondere hat man also:
|
Es gibt eine monotone und beschränkte Folge in , die gegen die irrationale Zahl konvergiert.
| [5.7.11]
|
Da nur einen Limes besitzen kann, ist in divergent!
|
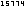 |
|